محاسبات آماری با اکسل
در اکثر نرم افزارهای محاسبات آماری، شاخص های مرکزی مانند میانگین و نما و همینطور شاخص های پراکندگی مانند واریانس و انحراف معیار محاسبه می شوند. چولگی و کشیدگی نیز از معیارهای تقارن برای توزیع داده ها محسوب می شوند. در این نوشتار به بررسی افزونه ای از اکسل می پردازیم که قادر به محاسبه این گونه شاخص های آماری است. برای نصب این افزونه که به نام Data Analysis معروف است، باید گام های زیر را مطابق با تصاویر مربوطه طی کنید. البته توجه داشته باشید که بسیاری از آزمون های و تحلیل های آماری نیز به کمک این افزونه قابل اجرا هستند.
گام اول: از فهرست File دستور Options را انتخاب کنید. پنجره ای به شکل زیر ظاهر خواهد شد. برای دسترسی به افزونه ها و نصب آن ها در اکسل، کافی است از کادر سمت چپ تصویر ۱، بخش Add-ins را انتخاب کنید. به این ترتیب در سمت راست پنجره، لیستی از افزونه های در حال اجرا (Active) یا غیرفعال (Inactive) ظاهر می شود.
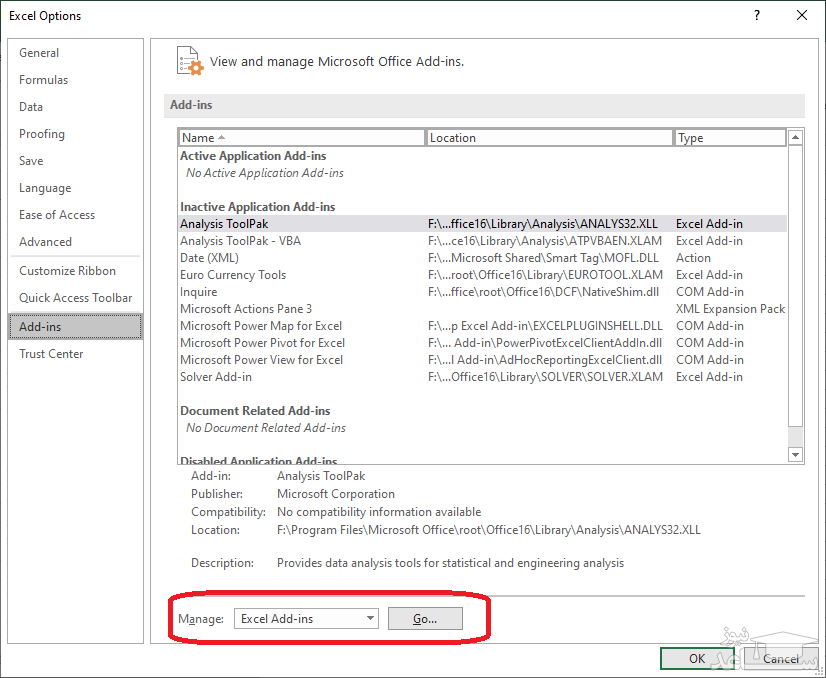
اگر می خواهید افزونه های غیرفعال را به صورت فعال در آورید، در بخش Manage گزینه Excel Add-ins را انتخاب و دکمه …Go را بزنید. به این ترتیب وارد گام دوم می شوید.
گام دوم: با طی کردن گام اول به پنجره Add-ins خواهید رسید که فهرستی از افزونه های فعال و غیر فعال را نشان می دهد. با انتخاب هر یک از افزونه ها در بخش یا فهرست Add-ins available، می توانید هر یک از آن ها را فعال یا غیرفعال سازید.
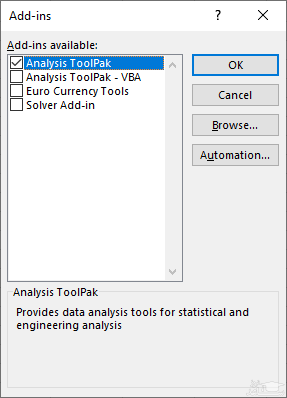
در تصویر ۲، برای فعال سازی افزونه محاسبات آماری در اکسل گزینه اول یعنی Analysis ToolPak را انتخاب کرده ایم. با فشردن دکمه OK عملیات بارگذاری این افزونه صورت خواهد گرفت.
با اجرای این گام ها، در برگه Data بخش جدیدی به نام Data Analysis ظاهر می شود. به این ترتیب با انتخاب این دکمه، پنجره ای مطابق با تصویر ۳ نمایان شده که می توانید نوع محاسبه و تحلیل آماری را از داخل آن انتخاب نمایید.
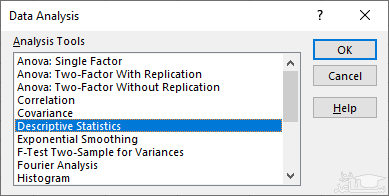
پس از انتخاب محاسبات دلخواه خود از این لیست، دکمه OK را بزنید. البته جدول ۱، گزینه های موجود در این پنجره را معرفی کرده است تا با انواع تحلیل های قابل اجرا آشنا شوید.
جدول ۱: لیست تحلیل های آماری در افزونه محاسبات آماری با اکسل
| ردیف | نام تحلیل | عملکرد | توضیحات |
|---|---|---|---|
| ۱ | Anova: Single Factor | تحلیل واریانس: تک عامل | تحلیل واریانس یک طرفه |
| ۲ | Anova: Two-Factor with Replication | تحلیل واریانس: دو طرفه | تحلیل واریانس دو طرفه با مشاهدات تکراری در هر سطح |
| ۳ | Anova: Two-Factor without Replication | تحلیل واریانس: دو طرفه | تحلیل واریانس دو طرفه بدون مشاهدات تکراری در هر سطح |
| ۴ | Correlation | ضریب همبستگی | محاسبه انواع شاخص های همبستگی دو متغیره |
| ۵ | Covariance | کوواریانس | تشکیل ماتریس کوواریانس |
| 6 | Descriptive Statistics | آمار توصیفی | محاسبه شاخص های آمار توصیفی |
| 7 | Exponential Smoothing | هموارسازی نمایی | روش پیش بینی سری زمانی با هموارسازی نمایی |
| 8 | F-Test Two Sample for Variances | آزمون F برای نسبت دو واریانس | آزمون آماری برابری واریانس دو جامعه آماری با استفاده از توزیع F |
| 9 | Fourier Analysis | تحلیل فوریه | حل سیستم های خطی با استفاده از تبدیل سریع فوریه |
| 10 | Histogram | هیستوگرام | رسم نمودار فراوانی (ستونی) |
| 11 | Moving Average | میانگین متحرک | هموارسازی و حذف روند از داده های سری زمان |
| 12 | Random Number Generation | تولید اعداد تصادفی | انتخاب توزیع آماری و استخراج یک نمونه با تعداد مشخص از آن |
| 13 | Rank and Percentile | رتبه و صدک ها | تحلیل برمبنای رتبه و محاسبه چندک های داده ها |
| 14 | Regression | رگرسیون خط | محاسبه ضرایب و فاصله اطمینان برای مدل رگرسیون خطی |
| 15 | Sampling | نمونه گیری | انتخاب یک نمونه تصادفی از بین مقادیر انتخاب شده |
| 16 | t-Test: Paired Two Sample For Means | آزمون t برای مقایسه میانگین زوجی | مقایسه تغییرات در اثر یک تیمار روی مشاهدات (آزمون قبل و بعد از اجرای تیمار) |
| 17 | t-Test: Two-Sample Assuming Equal Variances | آزمون t برای مقایسه میانگین دو جامعه مستقل | آزمون t برای دو جامعه مستقل با واریانس های برابر |
| 18 | t-Test: Two-Sample Assuming Unequal Variances | آزمون t برای مقایسه میانگین دو جامعه مستقل | آزمون t برای دو جامعه مستقل با واریانس های نابرابر |
| 19 | Z-test: Two sample for the Means | آزمون Z برای مقایسه میانگین | آزمون Z برای مقایسه میانگین دو جامعه مستقل با توزیع نرمال (معلوم بودن واریانس دو جامعه) |
به یاد داشته باشید که در این نوشتار به معرفی گزینه مربوط به محاسبات آمار توصیفی (Descriptive Statistics) پرداخته خواهد شد.
شاخص های آمار توصیفی به کمک افزونه محاسبات آماری با اکسل
از فهرستی که به عنوان گزینه های مختلف تحلیل های آماری معرفی شد، گزینه Descriptive Statistics یا محاسبات آمار توصیفی را برای محاسبات آماری با اکسل انتخاب کنید. پنجره جدیدی باز خواهد شد که ناحیه مربوط به مقادیر و همچنین شاخص های مورد نظر را از کاربر دریافت می کند. برای روشن تر شدن موضوع از یک کاربرگ اکسل که نمرات ۱۵ دانشجو در آن ثبت شده کمک می گیریم. این اطلاعات را در تصویر ۴ مشاهده می کنید.
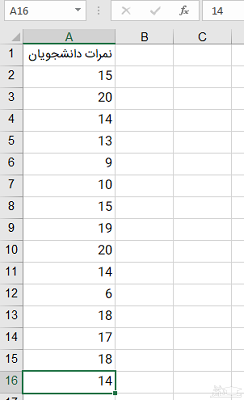
با توجه به ناحیه مربوط به اطلاعات این کاربرگ، پارامترهای آمار توصیفی را مطابق با تصویر ۵، تنظیم کرده ایم.
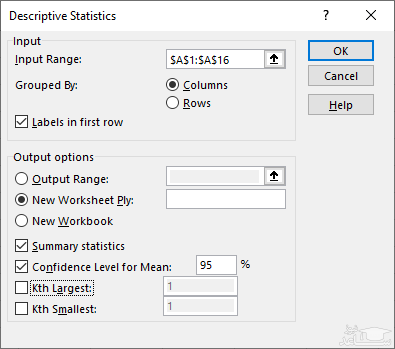
در قسمت Input Range، ناحیه ای از کاربرگ که باید شاخص های آمار توصیفی از آن استخراج شود، تعیین شده است. برای مثال ما این قسمت شامل ناحیه $A$1:$A$16 است. از آنجایی که گزینه Columns انتخاب شده است، متغیرها به صورت ستونی از مجموعه داده گرفته می شوند. از آنجایی که کاربرگ فقط شامل یک ستون است در نتیجه یک متغیر بیشتر برای تحلیل به کار نخواهد رفت.
نکته: اگر گزینه Rows را انتخاب می کردید، به تعداد سطرها، متغیر ایجاد می شد.
با فعال سازی گزینه Label in first row، اکسل متوجه می شود که سطر اول در ستون A، شامل نام متغیر است و نباید از آن در محاسبات استفاده کند. البته این سلول مقدار متنی دارد و در محاسبات نقشی نخواهد داشت.
بخش بعدی مربوط به تعیین محل خروجی محاسبات است. اگر گزینه Output Range را انتخاب کنید، باید ناحیه ای از کاربرگ را برای نمایش اطلاعات خروجی مشخص نمایید. با گزینه New Worksheet Ply یک کاربرگ جدید به منظور قرارگیری خروجی تعیین می شود. با گزینه New Workbook هم، کارپوشه ای جدید (یک فایل جدید اکسلی) برای نمایش اطلاعات جدول های آمار توصیفی در نظر گرفته خواهد شد.
اگر گزینه Summary statistics و Confidence Level for Mean را انتخاب کرده باشید، شاخص های معرفی شده در جدول ۲، محاسبه و در خروجی ظاهر خواهند شد.
نکته: انتخاب دو گزینه Kth Largest و Kth smallest باعث نمایش kامین مقدار بزرگتر و کوچکتر خواهد بود. مقدار K در کادر جلوی هر یک از این گزینه ها، وارد می شود.
جدول ۲: شاخص های توصیفی در خروجی محاسبات آماری در اکسل
| ردیف | شاخص | عملکرد | توضیحات |
|---|---|---|---|
| ۱ | Mean | محاسبه میانگین | شاخص مرکزی |
| ۲ | Standard Error | خطای استاندارد | انحراف استاندارد نمونه تقسیم بر جذر حجم نمونه |
| 3 | Median | میانه | مقدار مرکزی داده ها |
| 4 | Mode | نما | مقدار با بیشترین تکرار |
| 5 | Standard Deviation | انحراف استاندارد نمونه ای | جذر واریانس نمونه ای |
| 6 | Sample Variance | واریانس نمونه ای | میانگین مجموع مربعات انحراف از میانگین |
| 7 | Kurtosis | کشیدگی | معیار تقارن عمودی نسبت به توزیع نرمال |
| 8 | Skewness | چولگی | معیار تقارن افقی نسبت به توزیع نرمال |
| 9 | Range | دامنه تغییرات | فاصله بین حداقل و حداقل مقادیر |
| 10 | Minimum | کوچکترین مقدار | |
| 11 | Maximum | بزرگترین مقدار | |
| 12 | Sum | مجموع مقادیر | |
| 13 | Count | تعداد مقادیر | |
| 14 | Confidence Level(95.0%) | فاصله اطمینان برای میانگین نمونه ای | با سطح اطمینان ۹۵٪ (با توجه به انتخاب کاربر) |
با توجه به گزینه های انتخابی، خروجی اجرای این دستور که با فشردن دکمه OK در یک کاربرگ جدید ظاهر شده، مطابق با تصویر ۶ خواهد بود. همانطور که مشاهده می کنید، جدول و مقادیر متنوعی که برای شناخت رفتار داده ها لازم است توسط این افزونه محاسبه و طی یک گزارش ظاهر شده است.
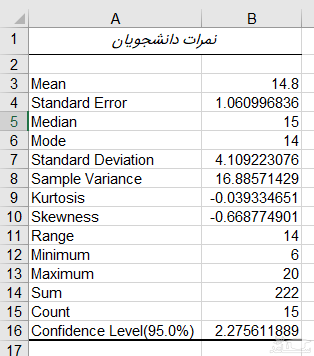
همانطور که مشخص است میانگین نمرات برابر با ۱۴٫۸ و انحراف استاندارد نیز تقریبا برابر با ۴ واحد است. در این صورت خطای برآورد میانگین حداکثر ۱٫۰۶ خواهد بود که نشان دهنده حداکثر یک واحد خطا برای میانگین نمرات کل دانشجویان در درس مورد نظر، توسط این نمونه تصادفی است.
همینطور چولگی و کشیدگی نیز به صفر نزدیک بوده که نشانگر تقارن و مشابهت توزیع این داده ها با توزیع نرمال (Normal Distribution) است.



 آموزش طراحی کارنامه با اکسل
آموزش طراحی کارنامه با اکسل