معمای یک، دو، سه، چهار!
می خواهیم بین دو نقطه حرکت کنیم به طوری که از هر یک از اعداد ۰ تا ۴ دقیقاً یک بار در طول مسیر گذر کنیم.
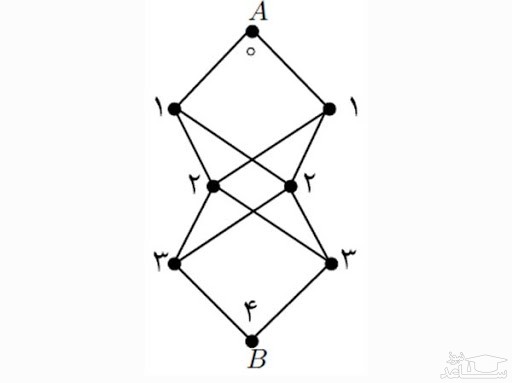
به شکل توجه کنید. به چند طریق می توان از نقطه ی A به نقطه ی B رفت به طوری که هر یک از اعداد ۰ تا ۴ دقیقاً یک بار در طول مسیر در نقطه ها مشاهده شوند؟
پاسخ معما
باید اعداد را به ترتیب صعودی طی کنیم زیرا در غیر این صورت از هر عدد دقیقا یک بار نمی توانیم بگذریم و عدد تکراری خواهیم داشت. حال برای رفتن از هر عدد به عدد بعدی مستقل از این که در کدام راس قرار داریم (به جز رئوس ابتدا و انتها) دو راه داریم پس در کل 23 یعنی ۸ مسیر وجود دارد.
معمای چراغ برق
در دو طرف خيابان اصلی شهر 18 چراغ برق در دو رديف 9 تايی مقابل هم نصب شده اند. فاصله بين دو چراغ متوالی پنجاه متر و عرض خيابان 10 متر است. بعضی از چراغ ها خاموش شده اما در فاصله کمتر از شصت متر از هر چراغ خاموش حداکثر سه چراغ خاموش ديگر وجود دارد. تعداد چراغ های خاموش حداکثر چندتاست؟
پاسخ معما
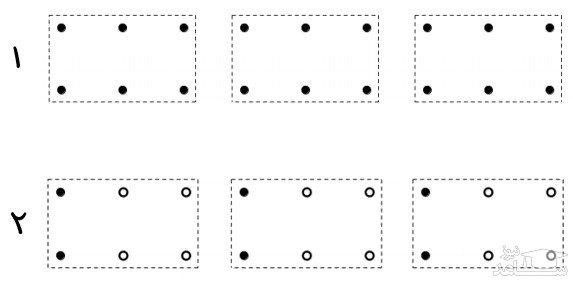
چراغها را مطابق شکل ۱، به سه دسته تقسيم میکنيم.
اگر در يک دسته بيشتر از ۴ چراغ خاموش باشد، پس يکی از دو چراغ وسطی اين آن دسته خاموش است. توجه کنيد از آنجا که اين چراغ از پنج چراغ ديگرِ همدسته اش فاصله ای کمتر از ۶۰ متر دارد، با اين فرض که در همسايگی ۶۰متری هر چراغ خاموش حداکثر سه چراغ خاموش ديگر قرار دارد تناقض دارد. پس در هر دسته حداکثر چهار چراغ خاموش داريم و بنابراين در کل حداکثر ۱۲ چراغ میتواند خاموش باشد.
شکل ۲ مثالی برای ۱۲ چراغ را نمايش میدهد. (دايره های توخالی چراغ های خاموش هستند.)
معمای لامپ های رنگی
9 لامپ در سه ردیف سه تایی قرار دارند. آن ها را با رنگ های قرمز، سبز، آبی و زرد رنگ می کنیم.
- در یک ردیف یا ستون، هیچ دو لامپی هم رنگ نیستند.
- لامپ وسط قرمز است.
- دقیقا یک لامپ سبز است.
حداقل تعداد لامپ های آبی چند است؟
پاسخ معما

در کل جدول حداکثر سه لامپ قرمز، سه لامپ زرد و یک لامپ سبز موجود است، بنابراین وجود دو لامپ آبی الزامی است.
معمای قورباغه
در برکه ای 7 قطعه سنگ وجود دارد که از چپ به راست با اعداد 1 تا 7 شماره گذاری شده اند.
قورباغه ای روی سنگ شماره یک نشسته است. فاصله سنگ ها به گونه ای است که اگر قورباغه روی سنگ i ام باشد می تواند حداکثر تا i سنگ جلوتر بپرد. به چند طریق ممکن است قورباغه، بدون برگشتن به سمت چپ، به سنگ شماره 7 برسد؟
پاسخ معما
روش اول: بیایید از آخر مسئله را حل کنیم. فرض میکنیم که در حال حاضر روی سنگ i-اُم هستیم و تعداد روش های مختلف برای رسیدن به سنگ 7اُم را یادداشت می کنیم. ابتدا مسئله را برای سنگ 7اُم حل می کنیم .
سپس برای سنگ 6اُم و ...
در هر مرحله کافی است که برای سنگ iاُم، مجموع تعداد روش های سنگ های 1 +i اُم تا 2i اُم را محاسبه کنیم. در نتیجه جواب مسئله اینگونه به دست می آید:
7:1 → 6:1 → 5:2 → 4:4 → 3:7 → 2:11 → 1:11
جواب 11 تا است.
روش دوم: استفاده از گراف های جهت دار و استفاده از ماتریس مجاورت آن است.
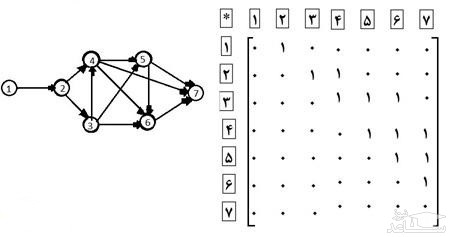
مسیر ها از 2 شروع می شوند در کل 11 مسیر داریم . قسمت 1 به 2 در همه مسیر ها مشترک است.
روش سوم:استفاده از الگویابی منظم
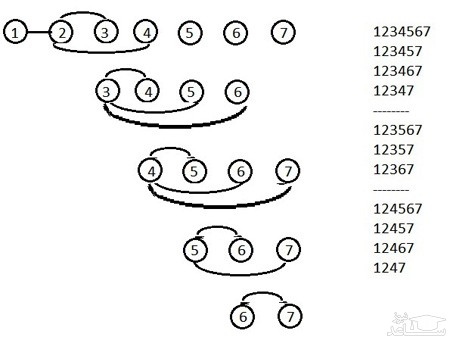
معمای همسایه های شطرنجی
آیا می توان 7 خانه از صفحه شطرنجی 8×8 را علامت گذاری کرد، به طوری که هر خانه علامت گذاری شده، با تعداد فردی از خانه های علامت گذاری شده همسایه باشد؟
(دو خانه تنها وقتی همسایه به حساب می آیند که یک ضلع مشترک داشته باشند)
پاسخ معما:
اگر a یا b در ضلع x همسایه باشد بدیهی است که در شمارش تعداد اضلاعی که باعث همسایگی دو خانه شده اند اضلاعی مانند x دو بار حساب می شوند. پس اگر تعداد کل اضلاع 7 خانه را که باعث همسایگی آنان با خانه های علامت گذاری شده ی دیگر شده اند را بشماریم باید زوج باشد. پس هر کدام از 7 خانه نمی تواند با تعداد فردی از خانه های علامت گذاری شده همسایه باشد. زیرا تعداد 7 تا عدد فرد هرگز زوج نمی شود.



 معما و تست هوش استخدام
معما و تست هوش استخدام