معماهای المپیادی
1. به جدول ۳×۳ پایین دقت کنید. در هر حرکت میتوانیم جای دو سطر یا جای دو ستون از این جدول را با هم عوض کنیم. با این حرکات به چند جدول گوناگون میتوان رسید؟
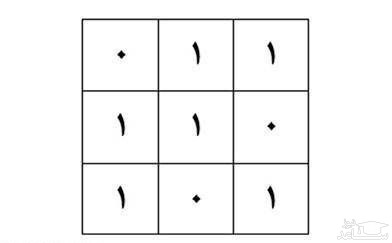
ب» ۱۲
ج» ۳۶
د» ۴۲
هـ» ۸۴
2. 5 گزاره در زیر آمده است. حداکثر چند تا از آنها می توانند با هم درست باشند؟
الف) اگر ب درست باشد آنگاه این گزاره غلط است.
ب) اگر تعداد گزاره های درست بیش تر از 2 باشد یکی از آنها پ است.
پ) حداقل یکی از الف و ت غلط است.
ت) ب و پ یا هر دو درست اند یا هر دو غلط.
ث) ب یا درست است یا غلط.
1) 3 2) 1 3) 4 4) 2 5) 0
3. شانزده مثلث داریم و می خواهیم آنها را با اعداد 0 یا 1 پر کنیم.
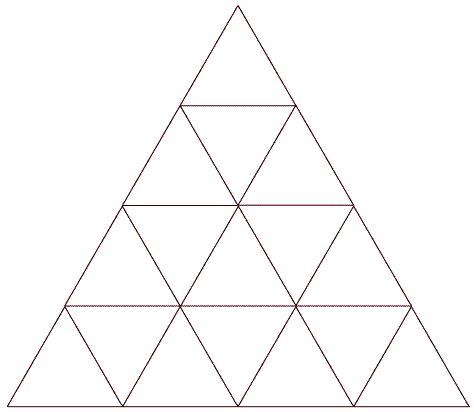
به چند طریق می توان همین کار کرد که مجموع اعداد موجود در مثلث های مجاور هر مثلث، زوج شود؟ (دو مثلث مجاورند اگر در یک ضلع مشترک باشند.) پاسخ های این دو سوال به ترتیب کدامند؟
الف) 1و 16
ب) 16 و 1
پ) 16 و 16
ت) 0 و 16
ث) 0 و 128
4. در برکه ای 7 قطعه سنگ وجود دارد که از چپ به راست با اعداد 1 تا 7 شماره گذاری شده اند.
قورباغه ای روی سنگ شماره یک نشسته است. فاصله سنگ ها به گونه ای است که اگر قورباغه روی سنگ i ام باشد می تواند حداکثر تا i سنگ جلوتر بپرد. به چند طریق ممکن است قورباغه، بدون برگشتن به سمت چپ، به سنگ شماره 7 برسد؟
الف) 10 ب) 11 ج) 12 د) 13
5. روستای شکرستان دزدی دارد که از دو سال پيش تحت تعقيب نظميه شکرستان قرار دارد. طبق تحقيقات نظمیه، تعداد سفرهای او بين شکرستان و ۴ نمکستان شرقی، غربی، شمالی و جنوبی به شکل فوق بوده است.
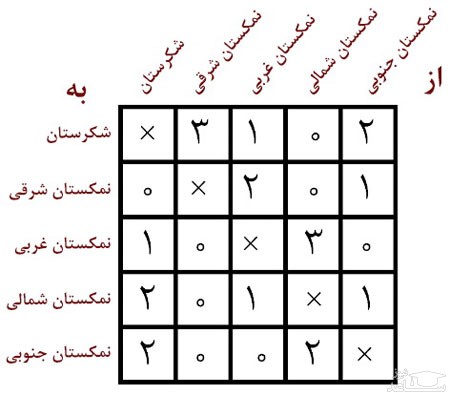
1) شکرستان
2) نمکستان شرقی
3) نمکستان غربی
4) نمکستان شمالی
5) نمکستان جنوبی
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
•°•
پاسخ معماهای المپیادی
1. انتخاب «الف» درست هست.
به سادگی قابل درک هست که هرگز با تعویض هاي یاد شده٬ دو عدد «۰» در یک سطر و یا در یک ستون قرار نخواهد گرفت. بنابراین در هر سطر و یا ستون دقیقا یک عدد«۰» و دو عدد «۱» وجود دارد. قرار دادن یک عدد «۰» در ستون اول به ۳ طریق ممکن هست. قرار دادن یک عدد «۰» در ستون دوم به شرطی که با «۰» موجود در ستون اول هم سطر نباشد
به ۲ طریق ممکن هست و بالاخره اینکه قرار دادن یک عدد «۰» در ستون سوم به شرطی که با هیچ یک از «۰» هاي قبلی هم سطر نباشد برابر ۱ می باشد که طبق اصل ضرب جواب مورد نظر 1×2×3 یعنی ۶ میشود.
2. گزینه «3» درست است.
واضح است که الف و ب نمی توانند با هم درست باشند (اگر با هم درست باشند طبق گزاره ی الف، الف باید غلط باشد که این تناقض است). بنابراین حداکثر 4 گزاره می توانند هم زمان درست باشند. از طرف دیگر همه ی گزاره ی ب تا ث می توانند با هم درست باشند. پس جواب همان 4 است.
3. گزینه (ت) درست است.
مثلث ها را مطابق شکل از 1 تا 16 نام گذاری می کنیم. در حالت اول که می خواهیم مجموع اعداد موجود در مثلث های مجاور هر مثلثی فرد باشد٬ چون تنها مثلث مجاور برای مثلث 1 مثلث 3 می باشد بنابراین علامت مثلث 3 برابر «1» می باشد. از طرف دیگر چون فقط دو خانه 3 و 6 مجاور خانه 2 می باشد بنابراین علامت خانه 6 برابر «0» می شود. به همین ترتیب علامت خانه 8 نیز «0» می شود. علامت خانه 13 برابر «1» و علامت خانه های 11 و 15 برابر «0» می شود که تناقض است.
در حالت دوم تمام مثلث های 13٬11٬8٬6٬3 و 15 علامت «0» را به خود می پذیرند. هریک از دسته مثلث های سه گانه 2٬1 و 4 نیز دسته مثلث های سه گانه 14٬9 و 16 به طور مستقل از یک دیگر به چهار طریق «0٬0٬0» یا «1٬1٬0» یا «0٬1٬1» و یا «1٬0٬1» قابل علامت گذاری می باشند و بقیه مثلث ها وابسته به این ها به صورت منحصربه فرد پر می شوند٬ بنابراین طبق اصل ضرب جواب مورد نظر 4×4 می باشد.
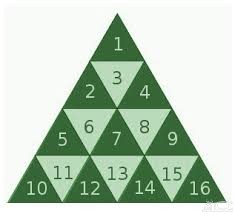
4. جواب گزینه ب 11 تا
روش سوم :
گزینه ی (ب) صحیح است.
بیایید از آخر مسئله را حل کنیم. فرض میکنیم که در حال حاضر روی سنگ i-اُم هستیم و تعداد روشهای مختلف برای رسیدن به سنگ 7اُم را یادداشت می کنیم. ابتدا مسئله را برای سنگ 7اُم حل می کنیم (1 روش).
سپس برای سنگ 6اُم و ...
در هر مرحله کافی است که برای سنگ iاُم، مجموع تعداد روشهای سنگهای 1 +i اُم تا 2iاُم را محاسبه کنیم. در نتیجه جواب مسئله اینگونه به دست می آید:
7:1 → 6:1 → 5:2 → 4:4 → 3:7 → 2:11 → 1:11
روش دوم: استفاده از گراف های جهت دار و استفاده از ماتریس مجاورت آن است
در زیر نگاه کنید
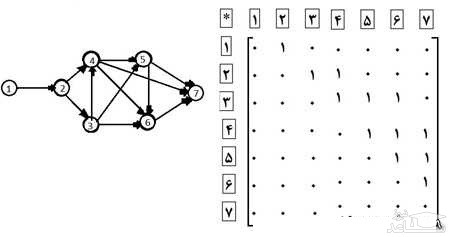
روش اول : استفاده از الگویابی منظم و رسم شکل است
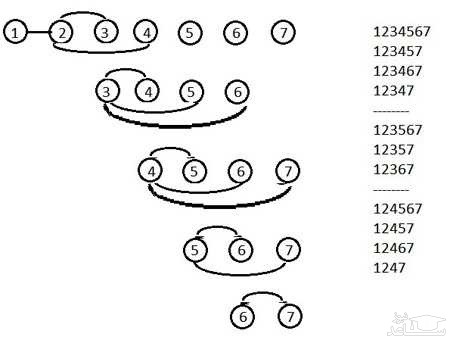
بنابراين او از شکرستان ۵ بار خارج شده است و ۶ بار به اين شهر برگشته است، بنابراين اکنون در اين شهر است و پاسخ درست گزينه ی (۱) است.

هم چنين با استدلال مشابه می توان فهميد که او سفر را از نمکستان شمالی آغاز کرده است، چون ۵ بار از اين شهر خارج شده و تنها ۴ بار به آن بازگشته است.


 معماهای جالب و تقویتی زاویه دید
معماهای جالب و تقویتی زاویه دید معماهای جالب و سخت برای ارتقای ضریب هوشی
معماهای جالب و سخت برای ارتقای ضریب هوشی